Seit den 80er Jahren werden vornehmlich im angelsächsischen Sprachraum so genannte Matrixkorrekturverfahren eingesetzt, um aus einer alten Verkehrsnachfragematrix und aktuellen querschnittsbezogenen Messwerten auf eine aktuelle Verkehrsnachfragematrix zu schließen. PTV hat aufbauend auf den Arbeiten von Van Zuylen/Willumsen (1980), Bosserhoff (1985) und Rosinowski (1994) diese vornehmlich IV-bezogenen Verfahren für den ÖV erweitert.
Ausgangspunkt des klassischen Verfahrens ist die Nachfrage auf den einzelnen Relationen fij. Sie wird üblicherweise in Matrixform notiert, aber für das hier diskutierte Verfahren empfiehlt sich die Darstellung als Vektor der Relationen mit von null verschiedener Nachfrage.
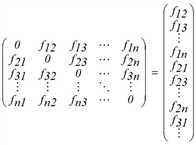
Während meist angenommen wird, dass eine auf einen früheren Zeitpunkt bezogene Matrix bekannt ist, liegt über den aktuellen Zustand nur partielle Information vor. Wichtig ist die Situation, in der insbesondere keine relationsfeinen Daten (aus einer Quelle-Ziel-Befragung) verfügbar sind, sondern nur Zählwerte an einzelnen Stellen im Netz. Dies können z.B. Quell-/ Zielverkehr oder Streckenbelastungen sein. Wir notieren die Zählwerte als einen weiteren Vektor.
cr = (c1 c 2 c3 ... cm)
Die Nachfrage jeder Relation liefert einen Beitrag zu den Zählwerten. Im Falle von Quell-/Zielverkehr sind z.B. die Randsummen der zu schätzenden Matrix bekannt. Streckenbelastungen entsprechen der Summe aller Relationen, die über die Strecke verlaufen. Allgemein zeigt folgende lineare Gleichung den Zusammenhang zwischen der Nachfrage und den Zählwerten:
A • f = c
wobei A die Anteilsmatrix genannt wird. Ein Element ask von A entspricht dem Anteil der Fahrten der Relation k, der das Zählobjekt (z.B. die Strecke) s befährt. Für Quell-/ Zielverkehr-Zählwerte hat A eine besonders regelmäßige Gestalt, wie am Beispiel für n = 3, m = 6 angegeben.
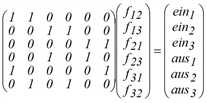
Insbesondere hängt in diesem Fall die Anteilsmatrix A nicht von der Umlegung ab. Für Streckenbelastungen geht dagegen die angebotsabhängige Wegewahl in A ein. Man erhält die Anteilsmatrix durch Umlegung einer vorhandenen Matrix (zum Beispiel der alten Nachfragematrix) auf das Angebot zum Zeitpunkt der Zählung. Beide Arten von Zählwerten lassen sich auch problemlos nebeneinander verwenden.
Problematisch bei der Matrixkorrektur ist, dass die Anzahl der Zählobjekte meistens deutlich kleiner ist als die Anzahl der Relationen, also m << n2, und damit die neue Matrix durch die Zählwerte unterbestimmt ist. Aus den unzähligen Matrizen, die auf die Zählwerte „passen“, wählt man daher die beste gemäß einer Bewertungsfunktion q aus, löst also das Optimierungsproblem:
max q(f), sodass A • f = c
Als Bewertungsfunktion dient oft eine Kombination aus Entropie und Gewichtung mit den Proportionen der alten Matrix. Die in Visum implementierte Bewertungsfunktion lautet:
wobei die die Werte der alten Matrix darstellen. q ist nichtlinear, weshalb das Problem iterativ gelöst werden muss.
Abbildung 68 zeigt für ein Beispiel, wie sich die Entropie in Abhängigkeit des geschätzten Matrixwertes ƒij ändert.
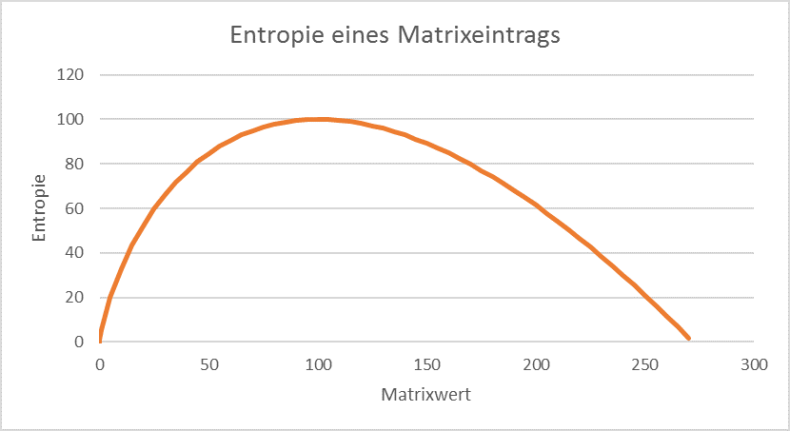
Abbildung 68: Die Entropie eines Matrixeintrags, dessen Originalwert 100 beträgt. Die maximale Entropie ist erreicht, wenn der Matrixeintrag identisch mit dem Originalwert ist.
In dieser Formulierung des Matrixkorrekturproblems liegt jedoch eine weitere Schwäche der klassischen Verfahren: der Vektor c der Zählwerte wird als bekannte Größe, frei jeder Unsicherheit, angenommen. Nur unter den Matrizen, die die Nebenbedingungen exakt erfüllen, wird eine q-maximale ausgewählt. Dadurch erhalten die Zählwerte ein unangemessenes Gewicht, denn jede Erhebung liefert eine Momentaufnahme, die mit einer Stichprobenunsicherheit behaftet ist. Klassische Verfahren (zum Beispiel von Willumsen) tragen diesem Umstand nicht Rechnung, da sie die Zählwerte als „scharfe“ Nebenbedingungen auffassen.
Deshalb hat PTV einen Ansatz von Rosinowski (1994) aufgegriffen, der die Zählwerte als unscharfe Messwerte ähnlich der Fuzzy-Sets-Theorie modelliert hat. Weiß man zum Beispiel, dass in einem Bezirk der Quellverkehr von Tag zu Tag um bis zu 10 % schwankt, in anderen Bezirken aber um 25 %, wird dies durch entsprechende Toleranzen t abgebildet. In den Nebenbedingungen des Matrixschätzproblems treten demnach unscharfe Bedingungen mit unterschiedlich großen Toleranzen an die Stelle scharfer Werte.
Dies wird erreicht, indem nicht negative Schlupfvariablen r und s eingeführt werden, wodurch die ursprüngliche Nebenbedingung ersetzt wird durch:
Hierbei sind die Vektoren und
definiert durch
und
, t ist der Toleranzvektor.
Ließe man es dabei bewenden, wären alle Ergebnisse zwischen und
erlaubt und in gleichem Maße bewertet, unabhängig davon, ob sie sich in der Mitte oder am Rand des Intervalls befinden. In Wirklichkeit favorisiert man aber ein Ergebnis in der Mitte des erlaubten Intervalls, weil dann der Zählwert genau getroffen wäre. Dieser ideale Fall tritt ein, wenn r = s = t.
Also werden für die Schlupfvariablen r und s entsprechende Entropie-Terme in die Bewertungsfunktion hinzuaddiert, wobei die Toleranzen t als Gewichtung dienen:
Veranschaulicht man die Entropie der Schlupfvariablen anhand eines Beispiels, kann man die Ähnlichkeit zu den Fuzzy-Mengen erkennen.
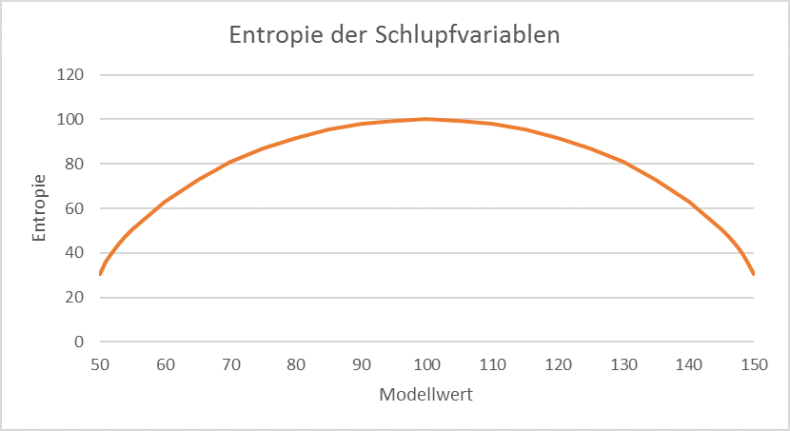
Abbildung 69: Als Beispiel stelle man sich einen Zählwert von 100 mit einer Toleranz von 50 vor. Mit Modellwert ist ein Wert des Vektors A•ƒ gemeint.
Die Entropie der Schlupfvariablen wird maximal, wenn der Zählwert genau getroffen ist, andernfalls nimmt sie zu den Rändern hin ab. Dies entspricht einer Fuzzy-Menge mit dem Intervall [50, 150] als Trägermenge und oben abgebildeter Zugehörigkeitsfunktion.
Die Darstellung als unscharfe Bedingungen gegenüber scharfen Schranken erlaubt also, die Bevorzugung zentraler Werte innerhalb der Trägermenge auszudrücken. Das heißt, im Allgemeinen werden Werte nahe dem Mittelwert der Zählwerte bevorzugt, akzeptiert werden aber auch Werte am Rand, wenn dadurch eine wesentlich geringere Abweichung von den Zählwerten erreicht wird.
Durch die Fuzzy-ähnliche Formulierung vergrößert sich der Lösungsraum des Schätzproblems und damit vergrößern sich die Freiheitsgrade für die Entropiemaximierung, sodass im Allgemeinen höhere Zielfunktionswerte erreicht werden. Anschaulich gesprochen wird somit die „wahrscheinlichste“ Nachfragematrix geschätzt, die die Zählwerte innerhalb der Bandbreiten nachbildet.

